Coriolis måleprinsipp

Ofte anvendte massestrømsmålinger bygger på prinsippet om Coriolis akselerasjon, eller det som er alminnelig anerkjent som Coriolis effekten. Denne teksten vil utdype oppfattelsen av Coriolis målingsteori, illustrert med eksempler og grafiske representasjoner for å formidle en grundig forståelse av denne flowmålingsteknikken.

Vi tilbyr Coriolis massestrømsmålere som håndterer fra svært lave verdier (50 mg/h) til mer omfattende mengder (600.000 kg/h).

Klikk her for å se vårt utvalg av Coriolisprodukter.

For å forstå Coriolis effekten bedre, la oss forestille oss jorden fra ekvators perspektiv, hvor vi observerer en stasjonær sky. Jordens rotasjonshastighet ved ekvator er omtrent 1600 km/t, en hastighet vi antar vår imaginære sky deler.
Anta nå at vår sky, under påvirkning av høy- eller lavtrykk, begynner å bevege seg nordover og til slutt når breddegraden 45°. På dette stedet har jorden en rotasjonshastighet på omtrent 1100 km/t, noe som skaper en differanse på rundt 500 km/t. Med friksjonsfaktorer satt til side, opprettholder skyen sin hastighet på 1600 km/t, noe som får den til å bevege seg raskere enn jorden.
Videre oppover, når skyen når Nordpolen, blir jordens overflatehastighet null, noe som fører til en hastighetsforskjell på rundt 1600 km/t mellom jorden og skyen. Således kan det sies at skyen blir satt i relativ bevegelse ift. jordoverflaten. På bakgrunn av Coriolis effekten vil værsystemer som oppstår ved ekvator og deretter beveger seg nordover ha en tendens til å skifte østover, og omvendt, de som beveger seg mot sør vil skifte vestover. Kort sagt, Coriolis effekten resulterer fra endringer i rotasjonshastigheten (vinkelhastigheten).

Coriolis masse flowmåling

m = r × A × n = r × V

Der:
m er massflow [kg/t]
r er tettheten (egenvekt) [kg/m³]
A er gjennomstrømnings arealet [m²]
n er strømningshastigheten [m/s]
V er volumstrømmen [m³/s]
v = massens hastighet

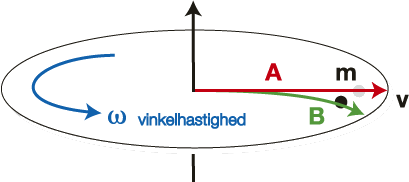
En masse m som beveger seg fra sentrum til periferien av en roterende sirkulær plate, vil bevege seg langs stien B. Hvis massen m føres i et rør A som er spent fast i hver ende, vil dette bøyes som en følge av Corioliseffektens kraft.

Coriolis masse flowmåling

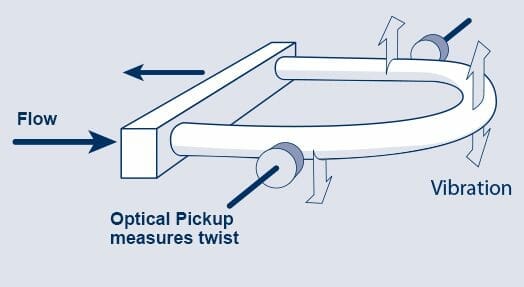
Coriolis-målerøret registrerer massestrømmen ved å tillate at mediet beveger seg gjennom de to bøyde målerørene som svinger frem og tilbake, for eksempel på 150Hz.
Hvis man har et fugleperspektiv på målerørene, vil strømmen av mediet som strømmer gjennom rørene minne om en sky som beveger seg fra ekvator og sørpå, og omvendt på slutten av målerørene.

Når mediet strømmer gjennom målerørene (som svinger i en pendelbevegelse), vil mediets masse motstå endringer i hastighet da det på vei inn i målerøret, og på samme vis motsette seg bremsing når den strømmer ut.
Bildene viser pendelbevegelsen til målerørene uten flow. Det er tydelig at målerørene er parallelle hele veien.

På bildet under, som viser den samme situasjonen, men med flow, kan man se en klar forskjell.
Målerørene vris i hjørnene når de svinger side til side. Dette skyldes mediets masse som motsetter seg de forandringene i fart som skjer under akselerasjon og deselerasjon ved henholdsvis inngangen og utgangen av målerørene.

Ved å installere to pickup-spoler, en ved inngangen og en ved utgangen av målerørene, kan vi kvantifisere vridningens grad i sammenligning med hverandre. Ved å måle den faktiske fasen mellom flow inn og flow ut, kan du bestemme massemengden som strømmer gjennom, siden denne variabelen er direkte korrelert med massestrømmen